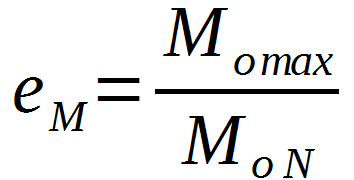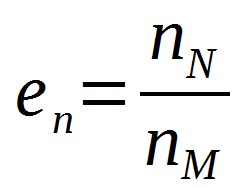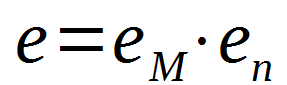Elastyczność silnika spalinowego to termin używany bardzo często, zarówno w prasie, jak i przez kierowców. Problem w tym, iż zwykle używa się tego określenia w sposób nieprawidłowy, a elastyczności jednostki napędowej zmierzyć się nie da. Da się natomiast wyliczyć tzw. wskaźnik elastyczności.
Elastyczność silnika to prawdopodobnie jedno z ulubionych określeń właścicieli turbodiesli. Nie da się ukryć, iż jednostki tego typu dysponują pokaźnym momentem obrotowym, dzięki czemu doskonale idą z dołu – czyli są w stanie dynamicznie przyspieszać choćby przy niskich prędkościach obrotowych silnika. Rzecz w tym, iż to tak naprawdę kilka ma wspólnego z definicją elastyczności, podobnie jak mierzenie jej stoperem. Bo elastyczność silnika spalinowego – a adekwatnie jej wskaźnik – się oblicza. I tak, oczywiście – wspomniany pomiar czasu przyspieszenia da jakieś pojęcie nt. elastyczności, ale tu słowo klucz: pojazdu, nie silnika. I to tylko w ściśle określonych warunkach. jeżeli pokażecie fizykowi tabelkę z danymi technicznymi, gdzie pod hasłem „Elastyczność” znajdzie czas przyspieszania od 80 do 120 km/h na najwyższym biegu, to możecie się spodziewać, iż ów fizyk tak was kopnie, iż osiągniecie drugą prędkość kosmiczną.
Co to jest elastyczność silnika? W jaki sposób wyliczyć jej wskaźnik?
Elastyczność silnika spalinowego to, według definicji, skłonność silnika do samoczynnego dostosowania się do zmieniających się warunków ruchu – czyli po prostu do zmieniającego się obciążenia. Żeby wyliczyć tzw. całkowity wskaźnik elastyczności (czyli ten, który nas najbardziej interesuje), trzeba najpierw mieć dane nt. wskaźnika elastyczności momentu obrotowego oraz nt. wskaźnika elastyczności prędkości obrotowej silnika.
Wskaźnik elastyczności momentu obrotowego wylicza się ze wzoru:
W liczniku podstawiamy tu maksymalny moment obrotowy silnika, a w mianowniku – moment obrotowy generowany przy obrotach mocy maksymalnej.
Dalej mamy wskaźnik elastyczności prędkości obrotowej:
Tutaj w liczniku podaje się prędkość obrotową, przy której silnik osiąga swoją maksymalną moc, a w mianowniku – obroty, przy których osiągany jest maksymalny moment obrotowy.
Gdy mamy już wyliczone oba te wskaźniki, można przystąpić do wyliczenia całkowitego wskaźnika elastyczności:
Jak prawdopodobnie wielu z was się teraz zastanawia, pierwsze dwa wzory wydają się być trudne do zastosowania w sytuacji, gdy dany silnik osiąga swoją maksymalną moc i moment obrotowy nie przy konkretnej prędkości obrotowej wału korbowego, ale w jakimś zakresie wartości obrotowych. W praktyce takie sytuacje miejsca nie mają, a fabryczne dane techniczne podawane są zawsze w mniejszym czy większym przybliżeniu. Jak więc to wszystko uwzględnić w wyliczeniach? To proste: zamiast wykresu przebiegu krzywych mocy i momentu zapewnianego czasem przez producenta auta (gdzie te krzywe są ładnie wygładzone i równiutkie), trzeba wziąć wykres wygenerowany podczas badania na hamowni podwoziowej.
Dla aut, gdzie maksymalną moc podaje się dla konkretnej prędkości obrotowej, można poprzestać na wykresie producenta – z tym zastrzeżeniem, iż otrzymany wynik może odrobinę odbiegać od rzeczywistego, osiąganego przez dany egzemplarz danego auta. Wykres nie jest jednak w takim przypadku niezbędny – jeżeli ktoś woli, można sobie przeprowadzić wyłącznie obliczenia, bez uciekania się do patrzenia na dane z hamowni. Po analizie powyższych wzorów widać, iż brakuje nam tylko jednego składnika: momentu obrotowego generowanego przy obrotach mocy maksymalnej. Wyliczymy go ze wzoru:
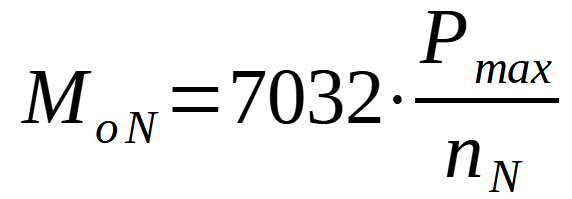 W liczniku po prawej stronie wpisujemy moc maksymalną danego silnika w koniach mechanicznych.
W liczniku po prawej stronie wpisujemy moc maksymalną danego silnika w koniach mechanicznych.Weźmy jakiś przykład do sprawdzenia. Tak się składa, iż sprzedawca pewnego Talbota Sunbeam Lotus z 1981 r., belgijski salon Lotusa z Oostende, był na tyle uprzejmy, iż sprawdził auto na hamowni i do zdjęć dołączył także wykres. Oto i on (uzupełnienia w kolorze czarnym naniosłem ja):
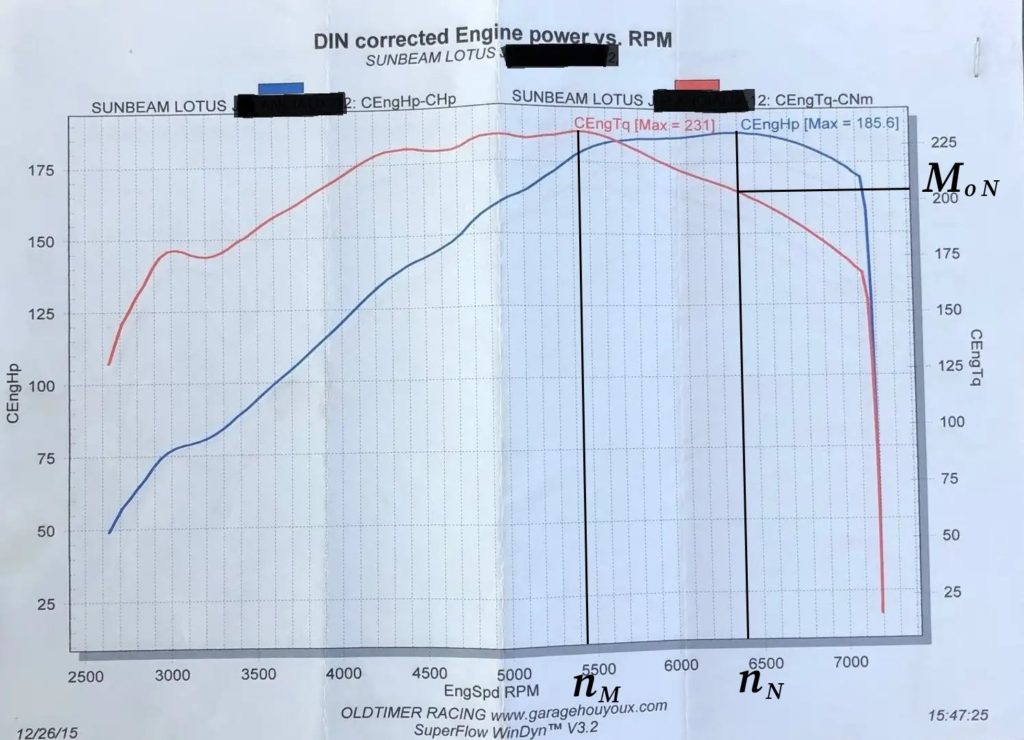 Zdjęcie pobrane z ogłoszenia. Dopiski i dorysowane czarne linie to moje dzieło. Fot. Lotus Oostende
Zdjęcie pobrane z ogłoszenia. Dopiski i dorysowane czarne linie to moje dzieło. Fot. Lotus OostendeCzyli tak: maksymalny moment obrotowy tego auta wynosi 231 Nm (informacja w kolorze czerwonym w górnej części wykresu). Przy obrotach mocy maksymalnej mamy natomiast 204 Nm (widać to na wykresie, tyle samo wychodzi też po skorzystaniu z powyższego wzoru). Wskaźnik elastyczności momentu obrotowego wynosi więc 231/204, co daje w przybliżeniu 1,132.
Idźmy dalej. Maksymalna moc (swoją drogą zauważalnie wyższa od fabrycznej, wynoszącej 152 KM) jest tu osiągana przy 6400 obr./min., a maksymalny moment obrotowy – przy około 5430 obr./min. Dzielimy: 6400/5430, co daje nam 1,179.
Całkowity wskaźnik elastyczności dla tego Sunbeama wynosi więc 1,132 x 1,179 = 1,335, co jest w praktyce wartością stosunkowo niską. Na ile niską? To się zaraz okaże, ponieważ przygotowałem dla was wyniki dla kolejnych kilkunastu aut z różnych klas, z silnikami benzynowymi i wysokoprężnymi, w obu przypadkach z doładowaniem lub bez.
Wskaźnik elastyczności silnika spalinowego – porównanie
W konkurencji udział biorą:
- para numer 1: Kia Rio (UB) 1.2 86 KM/121 Nm (R4, benzynowy, wolnossący) oraz 1.1 CRDi 75 KM/170 Nm (R3, turbodiesel),
- para numer 2: Fiat Tipo (Typ 356) 1.4 16V 95 KM/127 Nm (R4, benzynowy, wolnossący) oraz Fiat 500X (Typ 334) 1.3 JTD 95 KM/200 Nm (R4, turbodiesel),
- para numer 3: Mercedes W124 200E 109 KM/170 Nm (2.0 R4, benzynowy, wolnossący) oraz 300D 109 KM/185 Nm (3.0 R6, diesel, wolnossący),
- para numer 4: BMW 750i (E65) 367 KM/490 Nm (4.8 V8, benzynowy, turbodoładowany) oraz 745d 329 KM/750 Nm (4.4 V8, turbodiesel),
- para numer 5: Ford S-Max (WA6) 1.6 EcoBoost 160 KM/240 Nm (R4, benzynowy, turbodoładowany) oraz 2.0 TDCi 163 KM/340 Nm (R4, turbodiesel).
Do tego dorzućmy kilka bonusów:
- Cadillac Eldorado z 1976 r. (gaźnikowe 8.2 V8, 190 KM według normy SAE/488 Nm),
- McLaren F1 (6.1 V12, 627 KM/650 Nm),
- Bugatti EB 16.4 Veyron (8.0 W16 turbo, 1001 KM/1250 Nm).
Wszystkie powyższe wartości mocy i momentu obrotowego to dane fabryczne, zastosowane tu w celach poglądowych i dla pokazania, iż dobrałem auta o możliwie zbliżonych parametrach – można powiedzieć, iż postawiłem się w roli kupującego dany pojazd i rozpatrującego wersje o podobnych osiągach. Do większości wyliczeń skorzystałem jednak z danych odczytanych z wykresów z hamowni (a same wykresy dla wszystkich z powyższych aut wyszukałem w sieci) – wyjątkami są Mercedesy W124, gdzie do wyliczeń skorzystałem z wykresów zapewnionych przez producenta auta, oraz Cadillac i McLaren – dla tych aut obliczenia robiłem bez korzystania z wykresów.
Wyniki wyglądają następująco (w każdej parze podane są tylko całkowite wskaźniki elastyczności):
- Kia Rio 1.2 – 1,45, 1.1 CRDi – 2,07;
- Fiat Tipo 1.4 – 1,32, Fiat 500X 1.3 JTD – 2,01;
- Mercedes W124 200E – 2,39, 300D – 1,80;
- BMW 750i – 1,75, 745d – 1,83;
- Ford S-Max 1.6 EB – 2,98, 2.0 TDCi – 1,78;
- Cadillac Eldorado – 2,37,
- McLaren F1 – 2,02,
- Bugatti Veyron – 2,08.
Co mówią wyniki? Ano mówią na przykład to, iż turbodiesle mają przewagę nad wolnossącymi silnikami benzynowymi, co akurat wydaje się dość logiczne – przynajmniej do momentu gdy zauważymy, iż Kia Rio z 1,1-litrowym dieslem ma wyższy wskaźnik elastyczności niż McLaren F1. Gdy porównamy przykładowego wolnossącego benzyniaka z również wolnossącym dieslem (para Mercedesów W124), to okazuje się, iż to silnik benzynowy jest bardziej elastyczny – i to znacznie bardziej, choć w przypadku innych silników wyniki mogłyby być odwrotne. interesujące jest porównywanie silników z turbinami, bo czasem wygrywa diesel (BMW 7), a czasem benzyniak (Ford). Swoją drogą, Ford ze swoim całkowitym współczynnikiem elastyczności na poziomie 2,98 wygrywa z palcem w nosie całe to porównanie, choć gdybyśmy mieli mu mierzyć stoperem czas przyspieszania na wyższych biegach, to wypadłby marnie. Ba, powiem więcej: po ujrzeniu tej wartości, poszukałem innych wykresów z hamowni dla tego silnika i wyszły mi choćby wyniki rzędu 3,3…
Tak więc tak to wygląda, moi drodzy – 1,6-litrowy EcoBoost w moim Galaxy jest bardziej elastyczny od waszych diesli, od mocarnych silników w limuzynach BMW, a choćby od monstrum napędzającego Veyrona. Z tą świadomością i z uśmiechem na twarzy pójdę sobie teraz pojeździć.

 2 lat temu
2 lat temu